- Ecuación de Riccati
- En matemáticas, se llama ecuación de Riccati a toda ecuación diferencial ordinaria de la forma
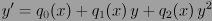 La ecuación toma su nombre del matemático veneciano Jacopo Francesco Riccati (1676-1754).
La ecuación toma su nombre del matemático veneciano Jacopo Francesco Riccati (1676-1754).
Enciclopedia Universal. 2012.
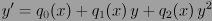 La ecuación toma su nombre del matemático veneciano Jacopo Francesco Riccati (1676-1754).
La ecuación toma su nombre del matemático veneciano Jacopo Francesco Riccati (1676-1754).Enciclopedia Universal. 2012.
Ecuación de Riccati — Saltar a navegación, búsqueda La ecuación de Riccati es una ecuación diferencial ordinaria desarrollada en el siglo XVIII por el matemático italiano Jacopo Francesco Riccati, con el fin de analizar la hidrodinámica. Corresponde a una ecuación de… … Wikipedia Español
Ecuación diferencial ordinaria — Saltar a navegación, búsqueda En matemáticas, una ecuación diferencial ordinaria (comúnmente abreviada EDO ) es una relación que contiene funciones de una sola variable independiente, y una o más de sus derivadas con respecto a esa variable. Las… … Wikipedia Español
Ecuación diferencial de Riccati — Saltar a navegación, búsqueda Jacobo Francesco Ricatti , matemático y filósofo, nació en Italia en 1676 conocido como conde y muere en 1754. Fue el principal responsable de la introducción de las ideas de Newton en Italia. En cierto momento, le… … Wikipedia Español
Riccati, Jacopo Francesco — ► (16761754) Matemático italiano. Resolvió la ecuación que lleva su nombre … Enciclopedia Universal
Jacopo Francesco Riccati — El conde Jacopo Francesco Riccati (Venecia, 28 de mayo de 1676 – 15 de abril de 1754) fue un matemático veneciano, que estudió detalladamente la hidrodinámica sobre la base de la mecánica newto … Wikipedia Español
Historia de las ecuaciones diferenciales — Una ecuación es una igualdad condicional que se cumple sólo para las soluciones de la misma. Así, en una ecuación algebraica como x – 2 = 0, la igualdad sólo se cumple para x = 2. En forma similar, una ecuación diferencial, constituida por… … Wikipedia Español
Función de Bessel — En matemática, las funciones de Bessel, primero definidas por el matemático Daniel Bernoulli y más tarde generalizadas por Friedrich Bessel, son soluciones canónicas y(x) de la ecuación diferencial de Bessel: (1) donde α es un … Wikipedia Español